Voxel Engine - Part 1 - Grids vs Octrees

I have been working on a voxel game engine written in C++ and OpenGL with the goal to render huge regions with enormous render distance in all 3 axis. For this to be possible, there must be some kind of level of detail so that not everything must be stored in memory. I also decided to use procedural generation so that at least the majority of the map information doesn’t need to be stored on disk.

Grids

At first I was storing voxels in a simple way: a 3D matrix of voxels, 4 bytes each, one for each color channel (red, green, blue, alpha). This allowed me to have a lot of different colors on the same mesh but I decided to make the voxels a single byte instead by just storing a material index. This way I would have a palette of up to 255 materials (0 represents no voxel) for the voxels and would enable me to add more properties to each voxel later on without any real impact on the memory used. This limits me to having 255 colors but it really isn’t that big of a problem because 255 is more than enough for the minimalistic look I’m targeting.

The problem of storing the world in a 3D matrix is that even if you have an enormous space completely empty or made from the same material, where every voxel is the same, it is still going to use a lot of memory. The obvious solution to this was using an octree.

Meshing

For the voxel grid to be rendered in a traditional way, we must first generate a mesh that represents the surface of the voxel volume. There are multiple ways to do it, the most obvious one being generating two triangles for each face of each non-empty voxel. The problem with this approach is that you end up generating a lot of geometry for faces that are always hidden (which in most cases is what happens to most of the faces). I ended up using a greedy meshing algorithm which merges multiple faces in order to decrease the total triangle count, which speeds up the rendering process. You can read more about it here.

This was the final result:

Octrees

In a voxel octree, you start with a large voxel which encapsulates completely the entire space that the grid would occupy. Then, you check if every smaller voxel inside of this larger voxel is equal. If they are all the same, the recursion stops. If they are not, this big voxel subdivides into 8 smaller voxels. This way, if you have a large empty area, it will use very little memory. The memory usage rises mainly not according to the size of the region with voxels, but according to the size of the voxel surface area.

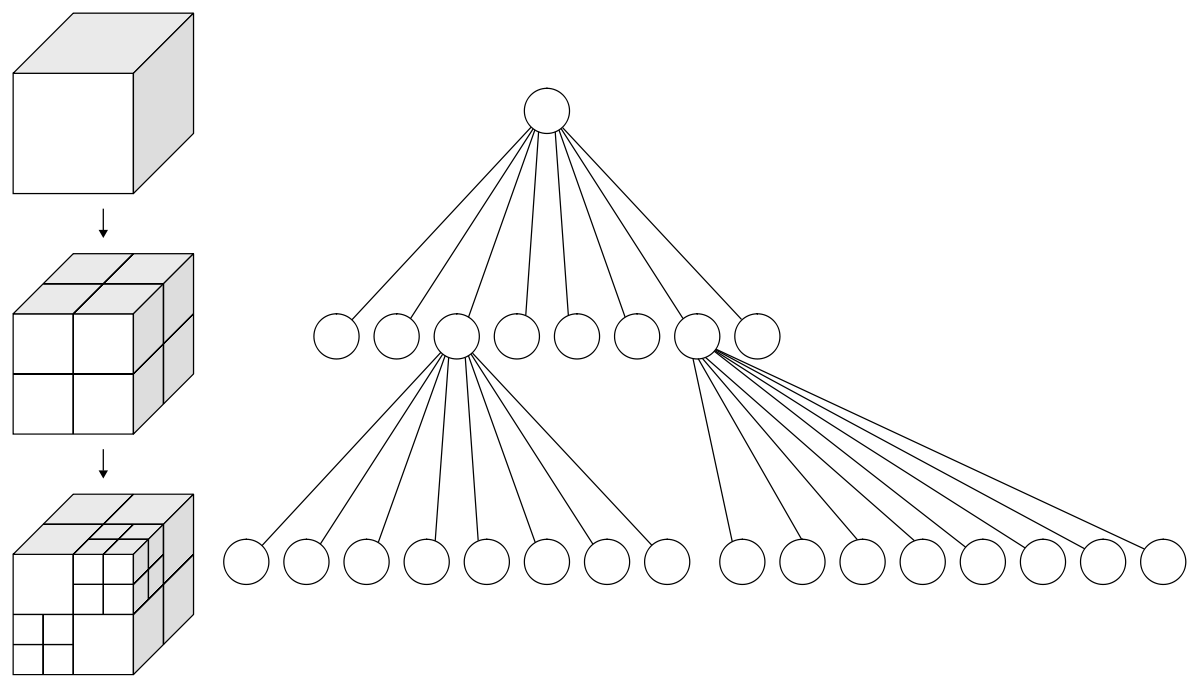
Instead of storing the voxels in a 3D matrix, in my octree implementation, the voxels are stored in a simple array. Each voxel stores an additional four bytes of data, an unsigned integer, that refers to the index of the first child of that voxel. If this index is 0, it means that the voxel is a leaf node, in other words, it means that the voxel isn’t subdivided. Sibling voxels are always stored in 8 voxel groups. This way, each voxel uses 5 bytes of memory, 5 times more than with a simple grid, but with this technique we store way less voxels in average, so it pays off in the end.

Meshing

Generating a mesh for an octree boils down to checking for each face of a leaf (non subdivided) voxel if there is a neighbour voxel hiding it or not. If there isn’t, the face is added to the final geometry. Octrees make LOD easier to implement. If we want to implement level of detail, we just need to stop the recursion at a certain level, even if the voxel is subdivided.

This was the final result of implementing this algorithm:

As you can see, way more vertices are generated this way when comparing it with the greedy meshing algorithm used on voxel grids (8 times more in average). The algorithm by itself generates the mesh two times faster, but in the end it doesn’t pay off.

Conclusion

Having all of this into account I have decided to take an ‘hybrid’ approach: instead of using just grids or octrees, I’m going to use an octree of grids. What this means is that, instead of having an octree where each node is a single voxel, each node would be a voxel grid (for example, a 16x16x16 grid). This way, LOD is still easy to implement, and I can still save a lot of memory, while generating meshes more efficiently at the same time.

When I finish implementing this, I will follow up this article with a second part.